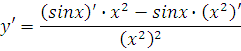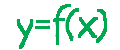
|
Автор: Сергей Смирнов
Как найти производную?Правила дифференцирования.
Чтобы найти производную от любой функции, надо освоить всего три понятия: 2. Правила дифференцирования. 3. Производная сложной функции. Именно в таком порядке. Это намёк.) Разумеется, неплохо бы ещё иметь представление о производной вообще). О том, что такое производная, и как работать с таблицей производных - доступно рассказано в предыдущем уроке. Здесь же мы займёмся правилами дифференцирования. Дифференцирование - это операция нахождения производной. Более за этим термином ничего не кроется. Т.е. выражения "найти производную функции" и "продифференцировать функцию" - это одно и то же. Выражение "правила дифференцирования" относится к нахождению производной от арифметических операций. Такое понимание очень помогает избежать каши в голове. Сосредоточимся и вспомним все-все-все арифметические операции. Их четыре). Сложение (сумма), вычитание (разность), умножение (произведение) и деление (частное). Вот они, правила дифференцирования:
В табличке приведено пять правил на четыре арифметических действия. Я не обсчитался.) Просто правило 4 - это элементарное следствие из правила 3. Но оно настолько популярно, что имеет смысл записать (и запомнить!) его как самостоятельную формулу. Под обозначениями U и V подразумеваются какие-то (совершенно любые!) функции U(x) и V(x).
Рассмотрим несколько примеров. Сначала - самые простые. Найти производную функции y=sinx - x2 Здесь мы имеем разность двух элементарных функций. Применяем правило 2. Будем считать, что sinx - это функция U, а x2 - функция V. Имеем полное право написать: y' = (sinx - x2)' = (sinx)'- (x2)' Уже лучше, правда?) Осталось найти производные от синуса и квадрата икса. Для этого существует таблица производных. Просто ищем в таблице нужные нам функции (sinx и x2), смотрим, какие у них производные и записываем ответ: y' = (sinx)' - (x2)' = cosx - 2x Вот и все дела. Правило 1 дифференцирования суммы работает точно так же. А если у нас несколько слагаемых? Ничего страшного.) Разбиваем функцию на слагаемые и ищем производную от каждого слагаемого независимо от остальных. Например: Найти производную функции y=sinx - x2+cosx - x +3 Смело пишем: y' = (sinx)' - (x2)' + (cosx)' - (x)' + (3)' Опять лезем в таблицу, находим там производные синуса, квадрата икса, косинуса, чистого икса и тройки. Что, тройки нет в таблице!? Ну да.) Тройка - постоянная величина, в таблице обозначена буквой "С". Производная любой постоянной величины равна нулю. Можно сразу записать ответ: y' = cosx - 2x - sinx - 1 Как видим, первые два правила дифференцирования просты и безотказны.)
Переходим к примерам на правило 3. Производная произведения чуть посложнее, да...) Главное здесь - увидеть в исходной функции, что взять за U, а что - за V. Например: Найти производную функции y=sinx · cosx. Здесь всё очевидно. sinx - это U, cosx - это V. Пишем прямо по правилу: y' = (sinx)' ·cosx + sinx · (cosx)' = cosx·cosx - sinx·sinx = cos2x - sin2x Вот здесь, частенько, возникает вопрос: оставить результат, как есть, или преобразовывать и упрощать дальше? Ответ зависит исключительно от задания и пожеланий преподавателя.) Производную мы уже нашли. Обычно, если упрощение простое и очевидное, его нужно сделать. В нашем случае получилась формула косинуса двойного угла. Можно написать ответ: y' = cos2x - sin2x = cos2x Рассмотрим следствие из правила 3, т.е. правило 4. Эта формула получается прямо из производной для умножения функций. Если y=CU, где С - какое-то постоянное число, а U - любая функция, то: y' =(C·U)' = C'·U + C·U' = 0·U + C·U' = C·U' Словами говорят, что постоянную можно вынести из под знака производной. Это маленькая, но очень полезная формулка. Позволяет делать кучу действий в уме. Например, по этому правилу все производные от выражений, типа 5х, 3,4х, -2х и так далее, сразу же превращаются в постоянные числа: (5х)' = 5·(x)' = 5·1 = 5 (-2х)' = -2·(x)' = -2·1 = -2 Ну, вы поняли.) Пример посложнее: Найти производную функции y=5sinx - 3x2. Если расписывать подробно, получится вот так: y' = (5sinx - 3x2)' = (5sinx)'- (3x2)' В скобках - произведения функций (постоянное число - тоже функция!). К первой и второй скобкам надо бы использовать правило 3, но сокращённый вариант (правило 4) - куда приятнее! Просто выносим числа за знак производной: y' = (5sinx)'- (3x2)' = 5(sinx)'- 3(x2)' Далее находим в таблице значения производных и результат просто умножаем на эти числа: y' = 5(sinx)'- 3(x2)' = 5cosx - 3·2x = 5cosx - 6x
Переходим к производной частного. Правило 5 - самое злое, да...) Расписывать да считать подольше приходится. Но... тут уж ничего не поделаешь. Против законов математики протестовать глупо.) Хотя, в качестве бонуса, помогу.) Расскажу, чуть ниже, о случаях, когда эту формулу применять не надо. Так как есть более простые варианты. А сейчас - пример: Найти производную функции
Расписываю по правилу 5. Подробно, со всеми скобочками и штрихами:
Берём производные (они табличные) в правой части:
Приводим к приличному виду:
Если требуется дальнейшее упрощение, можно в числителе вынести икс за скобки и сократить с иксом в знаменателе. Получим ответ:
Вот мы и рассмотрели, как находить производные функций с помощью правил дифференцирования.
Разумеется, сумма, разность, частное и произведение могут комбинироваться в самых разных сочетаниях. Например: Продифференцировать функцию: y=(x2+2) · (x3-4) Здесь под функцией U скрывается выражение (x2+2), а под функцией V - выражение (x3-4). Расписываем прямо по правилу: y' = (x2+2)' · (x3-4) + (x2+2) · (x3-4)' Теперь нужно довести дело до конца, т.е. вычислить производные от скобок. Штрих поставить - не означает "взять производную"...) В первых скобках будет сумма функций: (x2+2)' = (x2)' + 2' = 2x Во вторых - разность функций: (x3-4)' = (x3)' - 4' = 2x Можно записать ответ: y' = 2х · (x3-4) + (x2+2) · 3x2 Упрощаем, т.е. перемножаем и приводим подобные: y' = 2x4-8х + 3x4+6x2 = 5x4+6x2-8х Вот и всё. Достаточно производную от злой функции расписать подробно, со всеми скобочками и штрихами, по подходящему правилу. Затем последовательно брать производные от скобочек. Всё и получится.
Всё просто, но... могут случиться и сюрпризы. Попадётся, например, вот такое задание: Найти производную функции y=x3· sinx · cosx. Здесь у нас умножаются три функции. Нет подходящего правила. Ничего страшного. Нас спасут... скобочки!) Мы вправе превратить умножение трёх функций в произведение двух, чтобы правило 3 в дело запустить. Просто возьмём за U и V то, что нам нужно. Например, пусть U=x3· sinx Тогда V = cosx Выделим эти U и V скобочками в исходной функции: y=(x3· sinx) · (cosx). Скобки никак не меняют исходную функцию, можно брать производную по правилу 3: y'=((x3· sinx) · (cosx))'= (x3· sinx)'· (cosx)+(x3· sinx) · (cosx)' Теперь видно, что в скобках (x3· sinx)' у нас опять произведение функций. Но уже двух, что попроще.) Можно расписать производную этих скобок отдельно. Теперь за U у нас пойдёт x3, а за V - sinx: (x3· sinx)' = (x3)' · sinx +x3· (sinx)'= 3x2· sinx + x3· cosx Вот практически и всё. Возвращаемся к исходной функции и вставляем наш результат промежуточного дифференцирования на своё место. Сразу же и производную от косинуса во втором слагаемом возьмём: y'= (3x2· sinx + x3· cosx) · cosx + (x3· sinx) · (-sinx) Производную нашли. Если требуется, перемножаем скобки и записываем ответ: y'= 3x2· sinx · cosx + x3· cos2x - x3· sin2x Замечу, что в этом примере U и V можно было выбрать по другому. За U взять x3, а за V - sinx · cosx. Это без разницы. Результат будет тот же самый. Теперь - заслуженный бонус к правилу 5. В примерах постоянно приходится дифференцировать дроби. Что огорчает.) Но, если в знаменателе дроби - постоянное число, правила 5 можно избежать! Действия с дробями гласят, что деление можно заменить на умножение. Вот так:
Это даёт возможность вместо правила 5 использовать куда более простое и удобное правило 4. Например: Найти производную функции:
В процессе дифференцирования слегка преобразуем исходную функцию. Превратим деление в умножение:
Вот так. Арифметика из младших классов ещё никому не мешала!) Кстати, преобразование исходной функции перед дифференцированием вполне возможно и, иногда, очень помогает. Скажем, производная от функции:
берётся достаточно хлопотно. Таблицы производных и правил дифференцирования здесь недостаточно. Это сложная функция. Но если её преобразовать до дифференцирования, пример решается в уме. Как это сделать, написано в предыдущем уроке, пример № 3. В конце урока дам советы по облегчению жизни при дифференцировании.)
Практические советы: 1. Перед дифференцированием смотрим, нельзя ли упростить исходную функцию. 2. В замороченных примерах расписываем решение подробно, со всеми скобочками и штрихами. 3. При дифференцировании дробей с постоянным числом в знаменателе, превращаем деление в умножение и пользуемся правилом 4. Это помогает.)
<<<< Предыдущая страница: Что такое производная? Таблица производных
|
|
|||||||||||||||||||
|
||||||||||||||||||||