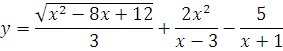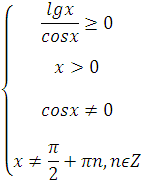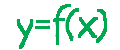
|
Автор: Сергей Смирнов
Область определения функции. Примеры.
В математике бесконечное множество функций. И у каждой - свой характер.) Для работы с самыми разнообразными функциями нужен единый подход. Иначе, какая же это математика?!) И такой подход есть! При работе с любой функцией мы предъявляем ей стандартный набор вопросов. И первый, самый важный вопрос - это область определения функции. Иногда эту область называют множеством допустимых значений аргумента, областью задания функции и т.п. Что такое область определения функции? Как её находить? Эти вопросы частенько представляются сложными и непонятными... Хотя, на самом деле, всё чрезвычайно просто. В чём вы сможете убедиться лично, прочитав эту страничку. Поехали?) В элементарном понятии функции фигурируют две величины. Независимая переменная (аргумент) x и зависимая переменная (функция) y. Так вот:
Все допустимые (разрешённые) значения аргумента x и есть область определения функции. И всё.
Достаточно разобраться в этой нехитрой фразе, как всё сразу становится на свои места. Что такое "допустимые значения"? Говоря по-простому, это те значения икса, для которых можно посчитать игрек. В принципе. Например, дана функция: y=3x-2 Можно посчитать игрек, скажем, для x=2? Легко! Получится y=4. А для x=1,2? Запросто. Получится y=1,6. Можно брать любое значение икса, целое, дробное, отрицательное, иррациональное - игрек всё равно посчитать можно. Точно, или приближённо, не суть важно. Нет никаких принципиальных запретов. Значит, для этой функции, все значения икса будут допустимыми. Значит, областью определения этой функции будут все действительные числа. Разумеется, функция может быть такой замороченной, что и не посчитаешь ничего, да... Это не страшно. Нам ведь не считать надо, а область определения найти). Чуть ниже мы научимся легко и элегантно расправляться с любыми функциями. Даже самыми злыми.) Слова "можно посчитать в принципе", "принципиальные запреты" я не зря употребил. Вот вам другой простенький пример. Дана функция: y=1/x Идём по проторенной дорожке. Для x=1 можно посчитать игрек? Конечно. А для x=0? Опаньки... Нельзя на ноль делить. Нет такой операции в математике! На любые числа делить можно, а на ноль - нельзя. Принципиально нельзя. Вот значение x=0 и будет недопустимым для этой конкретной функции. Стало быть, областью определения этой конкретной функции будут все числа, кроме нуля. Этот пример приведён чисто для понимания. Чтобы идею уловить. Разумеется, перебирать числа, задумчиво глядя на функцию, как-то глупо, да...) В математике так не делают. Правильный подход к области определения функции описан далее. Но сначала - одно важное замечание, чтобы потом не путаться. Область определения любой функции устанавливают: 1. Математика. Это законы и правила, которые всегда должны выполняться. Эти правила не зависят от нашего желания и вида задания. Они работают всегда. Область определения по этим правилам иногда называют "естественной". 2. Люди. Это дополнительные ограничения на область определения функции, которые могут быть (а могут и не быть) в любом конкретном задании и зависят исключительно от составителя задания. Самым важным является первый пункт. С него и начнём.
Как найти область определения функции?Итак, нам надо найти все допустимые значения икса для какой-то конкретной функции. Самый широкий набор значений, как правило - это все действительные числа. От -∞ до +∞. Перебирать все возможные числа мы не будем, да...) В математике поступают по-другому. Работаем в два этапа. На первом этапе ищем в функции операции, которые могут оказаться недопустимыми при каких-то значениях икса. Т.е. ищем потенциально опасные операции. На втором этапе определяем иксы, которые не приводят к запретному действию в этих самых операциях. Это и будет область определения функции. Если эти этапы не очень понятны, читаем дальше, на примерах всё куда яснее будет. Что такое потенциально опасные операции? Это операции, в которых существуют принципиальные ограничения. Не пугайтесь, таких операций всего ничего и вы их прекрасно знаете). Перечисляю: До 9-го класса включительно: 1. Деление. Нельзя делить на ноль. 2. Извлечение корня. Нельзя извлекать корни чётной степени из отрицательных чисел. В выпускных классах и ВУЗах: 3. Логарифмы. Ограничения в логарифмах: если logab = c, то а>0, a≠1, b>0. 4. Тригонометрия. Ограничения в тригонометрии: значения углов, для которых тангенс и котангенс не существуют, ограничения на выражения под знаком арксинуса, арккосинуса. Это, практически, весь набор потенциально опасных операций. Можно запомнить, правда?) Вот и всё, что надо знать, чтобы найти область определения любой функции. Теперь самое время применить эти знания в деле. Найдём область определения самой первой функции. Не перебором, а вполне научно): y=3x-2 Первый этап. Ищем в этой функции потенциально опасные операции. Деление есть? Деления нет. Корни? Корней нет. Логарифмы? Нет их. И тригонометрии тоже нет. В этой функции не может получиться никаких запретных действий. Какой бы икс мы не взяли. Этих действий в функции просто не содержится. Значит, ответ: х - любое число. Записывается ответ так: D(f)=(-∞;+∞) D(f) - это обозначение области определения функции. Как видите, в этом примере второй этап вовсе не понадобился. Бывает. Хорошая функция.) Следующий пример: y=1/x Опять ищем потенциально опасные операции. Такая операция есть. Деление. Не забыли, что дробь - это деление?) Переходим ко второму этапу. Определяем иксы, которые не приводят к запретному действию, т.е. делению на ноль. Собственно, к делению на ноль приводит лишь одно значение икса: x=0. Следовательно, все остальные значения безопасны. Областью определения функции будут все действительные числа, кроме нуля. В краткой записи: D(f)=(-∞;0) ∪ (0; +∞) Запись очень похожа на запись ответа для неравенств, правда? Всё верно. И там и здесь - запись промежутков числовой оси. Это были совсем простые примеры. Для знакомства). Переходим к более солидным заданиям.
Найти область определения функции:
Что, внушает?) Ничего не боимся и работаем по схеме. Выполняем первый этап: осматриваем функцию, на предмет потенциально опасных операций. Внимание! Мы ничего не решаем! Не упрощаем, не складываем дроби, не раскладываем на множители, не извлекаем корни, ни-че-го! Мы именно осматриваем функцию. Любые преобразования могут изменить область определения функции и мы получим неверный ответ. Сразу же выполняем и второй этап: то, что найдём в процессе осмотра, будем записывать, чтобы не забыть.) Итак, в первом слагаемом видим квадратный корень из выражения с иксом. Это потенциально опасная операция. Под корнем, при каких-то иксах, может оказаться отрицательное число. Обезопасим себя вот такой записью (второй этап): x2-8x+12 ≥ 0 Уловили? Квадратный корень извлекается только из положительных чисел и нуля. Всё подкоренное выражение должно быть больше, либо равно нулю. Не икс, а всё подкоренное выражение, целиком. Прошу заметить: в этой записи уже нет знака корня! А то так и норовят его написать... Корень нам не нужен, нас интересует только подкоренное выражение. Так, с корнем разобрались, идём дальше. В этом же слагаемом есть деление на 3. Игнорируем. Тройка - не икс, нулём стать не может.) Второе слагаемое. В нём есть деление на выражение с иксом. Знаменатель (весь знаменатель, целиком!) не может быть равен нулю. Записываем (второй этап): х-3 ≠ 0 Так, соломки подстелили, идём дальше. В третьем слагаемом опять есть деление. Записываем: х+1 ≠ 0 Ну, всё, функция кончилась.) Теперь сводим все наши записи в систему неравенств:
Система необходима, так как все наши условия должны выполняться одновременно. Осталось решить эту систему. В ответе получится как раз область определения этой функции. Ответ будет такой: D(f)=(-∞ ; -1) ∪ (-1; 2] ∪ [6; +∞) Как видим, функция может быть каким угодно монстром. Но в процессе осмотра и соответствующих записей мы получаем системку неравенств, которая вполне решаема. Так поступаем при нахождении области определения любой функции. Не знаете, как решать системы!? Ну, это вопрос не к функциям... Имейте в виду: задание как найти область определения функции почти всегда заканчивается решением системы неравенств... Как решать квадратные неравенства можно посмотреть по ссылке. Там, кстати, решено с пояснениями именно наше квадратное неравенство. Чисто случайно...) Последовательный осмотр и запись системы неравенств обычно особого труда не составляют. Хуже, когда потенциально опасные операции ещё и наслаиваются друг на друга. Здесь требуется пристальное внимание, чтобы чего не упустить. Например:
Найти область определения функции:
На первом этапе замечаем квадратный корень. Сразу пишем условие для всего подкоренного выражения:
Так, квадратный корень обезопасили. Но двигаться дальше ещё рано. Внутри корня есть ещё две потенциально опасные операции! Логарифм и деление. Для логарифма записываем:
Для деления записываем:
Вот теперь первое слагаемое разобрано по косточкам. Можно двигаться дальше. Для тангенса нужно записать:
Вот и всё. Сводим все наши записи в систему:
Система получилась не самая простая. Так и функция - приличного уровня. Предполагается, что студенты, которые сталкиваются с подобными функциями, решать системы неравенств умеют.) В этом уроке главное - освоить, как задачу "найти область определения функции" свести к задаче "решить систему неравенств". Повторю алгоритм ещё раз: 1. Работаем с исходной функцией! Ничего не упрощаем и не преобразовываем! Это всё делаем (если надо будет) после нахождения области определения. 2. Внимательно осматриваем функцию на предмет потенциально опасных операций. 3. В процессе осмотра записываем в систему неравенства, которые обеспечивают допустимость опасных операций. 4. Решаем систему неравенств и записываем ответ. Самые внимательные, наверняка, почувствовали схожесть этого процесса с нахождением области допустимых значений (ОДЗ). Ну, что тут сказать... Только респект.) Да! Естественная область определения функции (о которой здесь идёт речь) совпадает с ОДЗ выражений, входящих в функцию. Соответственно, и ищутся они по одним и тем же правилам. А сейчас рассмотрим не совсем естественную область определения.)
Дополнительные ограничения на область определения функции.Здесь речь пойдёт об ограничениях, которые накладываются заданием. Т.е. в задании присутствуют какие-то дополнительные условия, которые придумал составитель. Или ограничения выплывают из самого способа задания функции. Что касается ограничений в задании - тут всё просто. Обычно, и искать-то ничего не надо, всё в задании уже сказано. Напомню, что ограничения, написанные автором задания, никак не отменяют принципиальные ограничения математики. Нужно просто не забыть учесть условия задания. Например, такое задание: Найти область определения функции:
на множестве положительных чисел.
Естественную область определения этой функции мы нашли выше. Эта область: D(f)=(-∞ ; -1) ∪ (-1; 2] ∪ [6; +∞) А теперь учитываем дополнительные ограничения. Слова "на множестве положительных чисел" означают, что иксы могут быть только положительные. Вместо этих слов может быть задано условие "где x>0", или "где х ∈ (0; +∞)". Если наложить это ограничение на ответ, получим новую область определения: D(f)=(0; 2] ∪ [6; +∞) Вот и все дела. Всё предыдущее относилось к области определения аналитически заданных функций. Это самые популярные функции. Но существуют и другие способы задания функции. Они менее привычны и могут поставить в тупик. Во избежание таких фокусов, кратенько пробежимся по D(f) для функций, заданных НЕ аналитически. В табличном способе областью определения функций будут только те значения икса, которые даны в таблице. Других иксов для такой функции просто не существует. Разумеется, если в задании будут дополнительные ограничения на D(f), их надо будет учесть. Но основным источником информации будет таблица. В графическом способе основной источник информации - график. Его нужно уметь читать и знать, что означают всякие точки и кружочки на рисунке.) Например, задание:
Найти область определения функции у=f(x):
Ни одной формулы нет, да... Только график. Вспоминаем, что область определения функции - это допустимые значения иксов. Вот и смотрим, для каких иксов существует нарисованная на графике функция? Наводим мышку на рисунок (или касаемся картинки на планшете) и видим, что вся кривулина укладывается между значениями -6 и 6. Левее -6 и правее +6 никакой функции нет. Найти значение функции, скажем, для х=8, невозможно. Не существует там функция. Стало быть, говорить о D(f) можно только на промежутке от -6 до +6. Остаётся понять: входят ли концы промежутка в область определения функции, или нет? Эта информация тоже имеется на графике. Для значения х=-6 на кривой отмечена незакрашенная точка. Белая. Такие точки называют выколотыми. Это означает, что в этой точке функция не существует. Вот для х=-5,99999.... функция ещё существует, а для х=-6 - уже нет. Следовательно, значение х=-6 не включается в D(f). При значении х=+6, на графике отмечена закрашенная точка. Это значит, что при х=+6 функция существует. Этот икс необходимо включить в D(f). Вот и всё. Ответ: D(f)=(-6; +6] В словесном способе задания функции нужно внимательно читать условие и находить там ограничения на иксы. Иногда глаза ищут формулы, а слова свистят мимо сознания да...) Пример из предыдущего урока: Функция задана условием: каждому значению натурального аргумента х ставится в соответствие сумма цифр, из которых состоит значение х. Здесь надо заметить, что речь идёт только о натуральных значениях икса. Тогда и D(f) мгновенно записывается: D(f): х ∈ N
Как видите, область определения функции - не такое уж сложное понятие. Нахождение этой области сводится к осмотру функции, записи системы неравенств и решению этой системы. Конечно, системы бывают всякие, простые и сложные. Но... Открою маленький секрет. Иногда функция, для которой надо найти область определения, выглядит просто устрашающе. Хочется побледнеть и заплакать.) Но стоит записать систему неравенств... И, вдруг, системка оказывается элементарной! Причём, частенько, чем ужаснее функция, тем проще система... Мораль: глаза боятся, голова решает!)
<<<< Предыдущая страница: Способы задания функции.
|
|
||||
|
|||||